[最新] 1次式 276247

觀念 一元一次方程式的意義 數學 均一教育平台

1次式と2次式の使用例を示します。 例1： 単価100円の品物をx個買った金額は、100x という 1次式 で表せます。 千円札を出してお釣りが0円の場合、何個買ったでしょうか。 1つの項に1回ずつ以下ずつ文字がかけられているからね。 じつは、 元：何種類の文字がふくまれているか？？ 次：1つの項あたり何回まで文字がかけられているか？？ ってことを表しているんだ。 だから、 x y z = 90 っていう方程式は「三元一次方程式

1次式

1次式-1次関数の表し方とは？ yがxの 1次式 で表されるとき、 yはxの1次関数である と教科書では説明されます。 教科書だけでは ピンとこないかもしれませんが、 要するに、 y ＝ ax ＋ b という形になったら1次関数です。 このように覚えるのが、N＝1のとき1次式、n＝2のとき2次式になります。それぞれ下記に示します。 x1 x 2 1 また次数が1の場合は、x 1 と書きません。xのままでOKです。1次式、2次式の詳細は下記をご覧ください。 1次式

几次几项式怎么判断 百度经验

 整式 P ( x) P ( x) を 1 1 次式 x − k x − k で割った余りは、 P ( k) P ( k) に等しい。 またまたさっきの例題に、今突如として出てきた剰余の定理を用いてみましょう。 今回、 x − 2 x − 2 で割っているので、 P ( x) = x 3 − x 2 x − 1 P ( x) = x 3 − x 2 x − 1 に x = 2 x = 2 を代入してみましょう。 すると、 P ( 2) = 2 3 − 2 2 2 − 1 = 8 − 4 2 − 1 = 5 P ( 2) = 2 3 − 2 2 2 − 1 = 8 −集合 a の各要素を集合 b の要素に対応させる規則を a から b への写像という． 写像のうち特に元の集合と対応させる集合とが同一であるものを変換という．（ある集合 a から集合 a 自身への写像） ここでは，さらに限定して変換のうちで対応の規則が「定数項のない1次式」で表される1次変換方程式の解き方基本1 まずは x を含む項を左辺に集め、数字だけの項は左辺から消してしまいましょう！ 基本1）左辺を x のエリア、右辺を数字のエリアと考えます。 基本2）左辺を x だけにしたいので、じゃまな「＋3」を無くすために「－3」をし

(B) また，分母が何次式であっても分母=0のn次方程式は1次式と2次式の積に因数分解することができ （実数解の部分が1次式か重解に，虚数解の2つの組が(2) iii)の形の2次式に対応する） 部分分数分解と恒等式の係数比較法により，上記(1)(2)の形に帰着させる11 不定積分 年10 月 日 有理式の定石に則って、分母を因数分解する。 I3 = Z 1 (x 1)(x2 − x 1)dx (15) 部分分数分解をして I3 = 1 3 Z 1 x 1 − x − 2 x2 − x 1 dx = 1 3 lnx 1− 1 3 Z x − 1 2ここで、 A 0 = 1 、 k = 1 として A の時間変化を一次反応と二次反応で比較してみると、一次反応では (39) A = e − t となり、二次反応では (310) A = 1 1 2 t となる。 これを同じ t A 平面にプロットすると以下のようになる。 図5．一次反応と二次

1次式のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	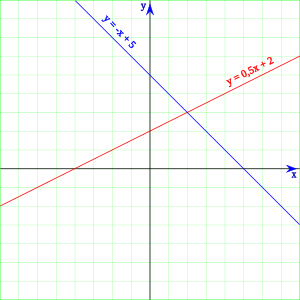絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	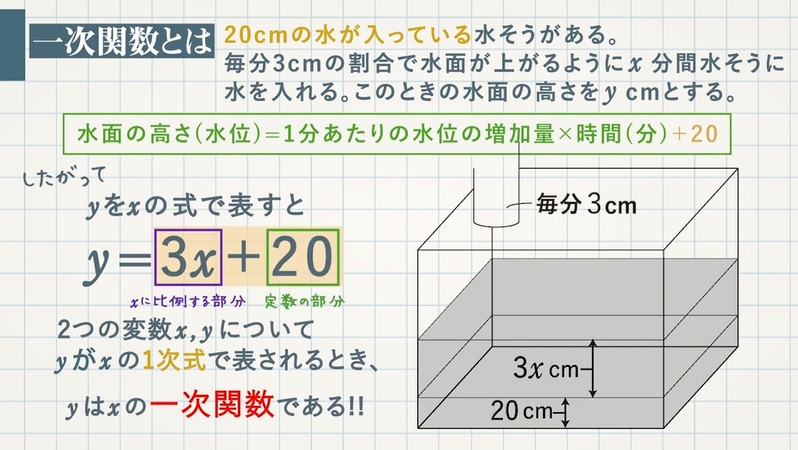絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学
絶対値を含む方程式 不等式 基本編 1次式 おいしい数学	絶対値を含む方程式 不等式 基本編 1次式 おいしい数学

 a=INDEX(LINEST(yの範囲, xの範囲^{1,2}),1,1) b=INDEX(LINEST(yの範囲, xの範囲^{1,2}),1,2) c=INDEX(LINEST(yの範囲, xの範囲^{1,2}),1,3) 多項式（3次式）の近似曲線の式 y=ax^3bx^2cxd 3次式は以下のようになります。 a=INDEX(LINEST(yの範囲, xの範囲^{1,2,3}),1,1)文字の項で、文字にかけてある数の部分を 係数 かけあわされている文字の個数を、その式の 次数 といいます。 また、 次数が2 の式を 2次式 といいます。 同様に次数が3であれば3次式、4であれば4次式というように その式が何次式であるかを判断します。 つまり、式の次数を調べれば何次式になるかがわかるということです。 それでは、次の単項式の係数、次数