√1000以上 角の二等分線 264713-角の二等分線の長さ
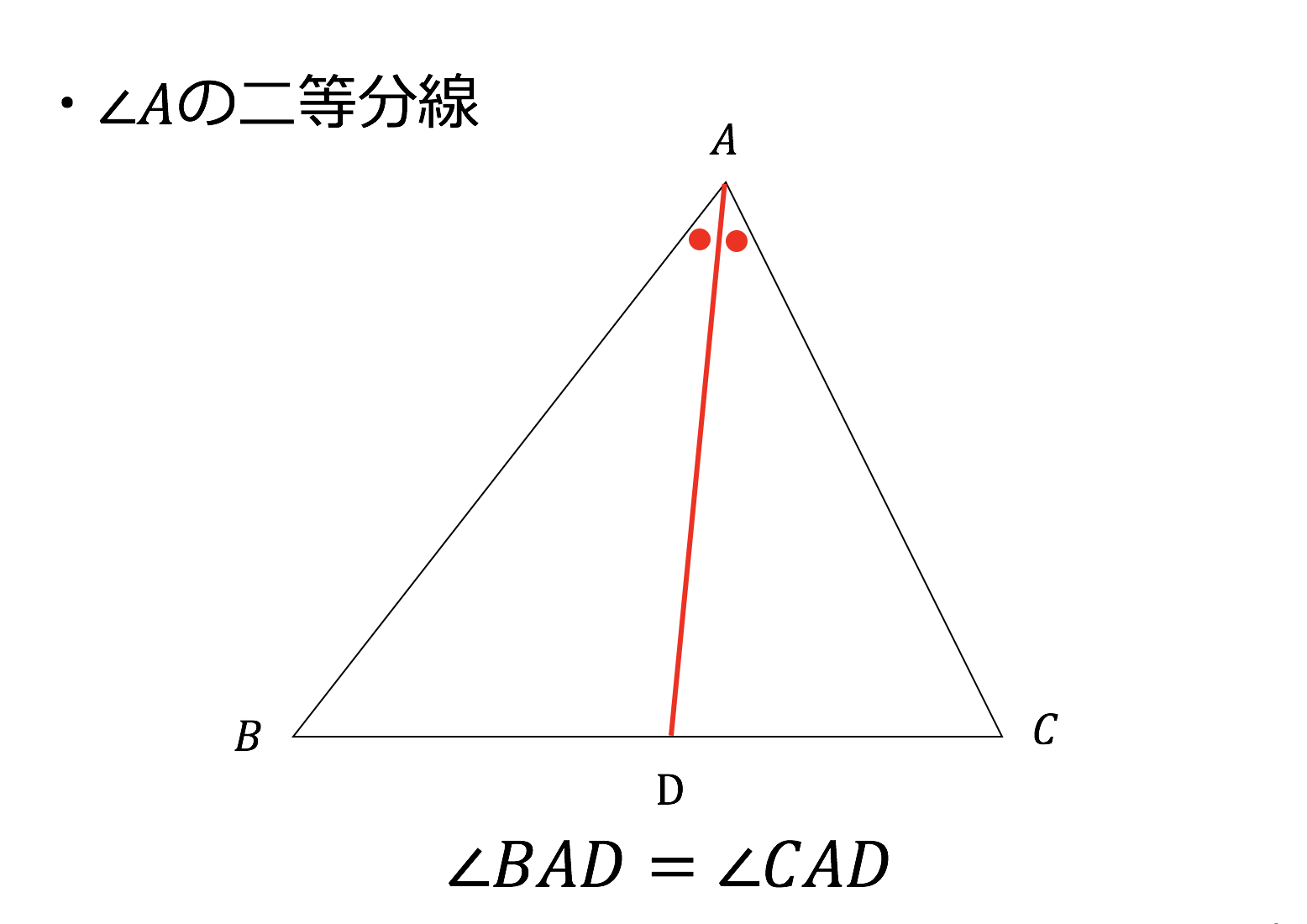
・二等辺三角形の等辺を挟む角の二等分線は、対辺の垂直二等分線である。およびその逆。 ・ある線分の両端と、その線分の垂直二等分線上の任意の点で、三角形が出来るとき、 それは二等辺三角形である。 ・中点連結定理 などは、既知のこととします。 重心 三角形の3本の中線は一点で 数学角の二等分線にまつわる絶対に覚えておきたい公式 ~受験の秒殺テク(8)~ 角度or長さの比を楽に出せるテクニック 今回は角の二等分線が引かれている問題と出会ったとき、必ず思い出せるようにしておきたい公式をいくつか勉強していきましょう。日本大百科全書(ニッポニカ) 二等分線の用語解説 角の頂点を通ってその角を同じ大きさの角に分ける直線を角の二等分線という。二等分線上の点で角の内部にある点から角の二辺へ至る距離は等しい。角の二等分線を作図するには、角の二辺の上に頂点から等距離にある点をとり、その2点を
角の2等分線
角の二等分線の長さ
角の二等分線の長さ- 「角の二等分線」と平行な直線を引いて baの延長した直線の交点をeとします ここでできる aceが 「二等辺三角形」である ことを利用して 「平行線と線分の比」 を使って 証明することができます 練習問題 角の二等分線定理 「左:右=左:右」で 覚えましょう を利用して 比例式を 角の二等分線定理で終わりそうです。 教科書にはあると思うけど外角の二等分線について少し説明しておきます。 ここは読み飛ばしても大丈夫ですよ。 証明方法は1つではありませんので後で確認する程度で、先ずは使えるようになりましょう。 一般性は失われないのでab>acとして



内接円 内心
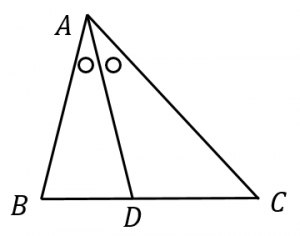
三角比と角の二等分線 角の二等分線とは、角を同じ大きさに分ける線のことです。下の図で言うと、 AD が $\angle \mathrm{ A }$ の二等分線です。 有名な性質として、 $\mathrm{ AB }\mathrm{ AC }=\mathrm{ BD }\mathrm{ CD }$ になる、というものがあります。 次のように、 C を通り、 AD に平行な線をひくとPage 1 高校で教えたい幾何の問題 角の二等分線の性質を狩る 札幌旭丘高校 中村文則 はじめに 三角形ABC の頂角Aの二等分線を,正確に引けない生徒が意外と多いことに驚く. 辺BC の中点と交わり、なぜか中線になってしまう.「角の二等分」から「辺の二等分」へと安易に結び 角の二等分線の求め方 1 tanの加法定理で求める →発想は単純ですが意外と大変かもしれません。 2 点と直線の距離の公式を使う →この解法を理解してほしいところです。 広告 例題 O(0,1),A(2,5),B(5,16)とするとき∠AOBの二等分線の方程式を求めよ。 解法1 tanの加法定理 OAとx軸のなす角をα,OBと
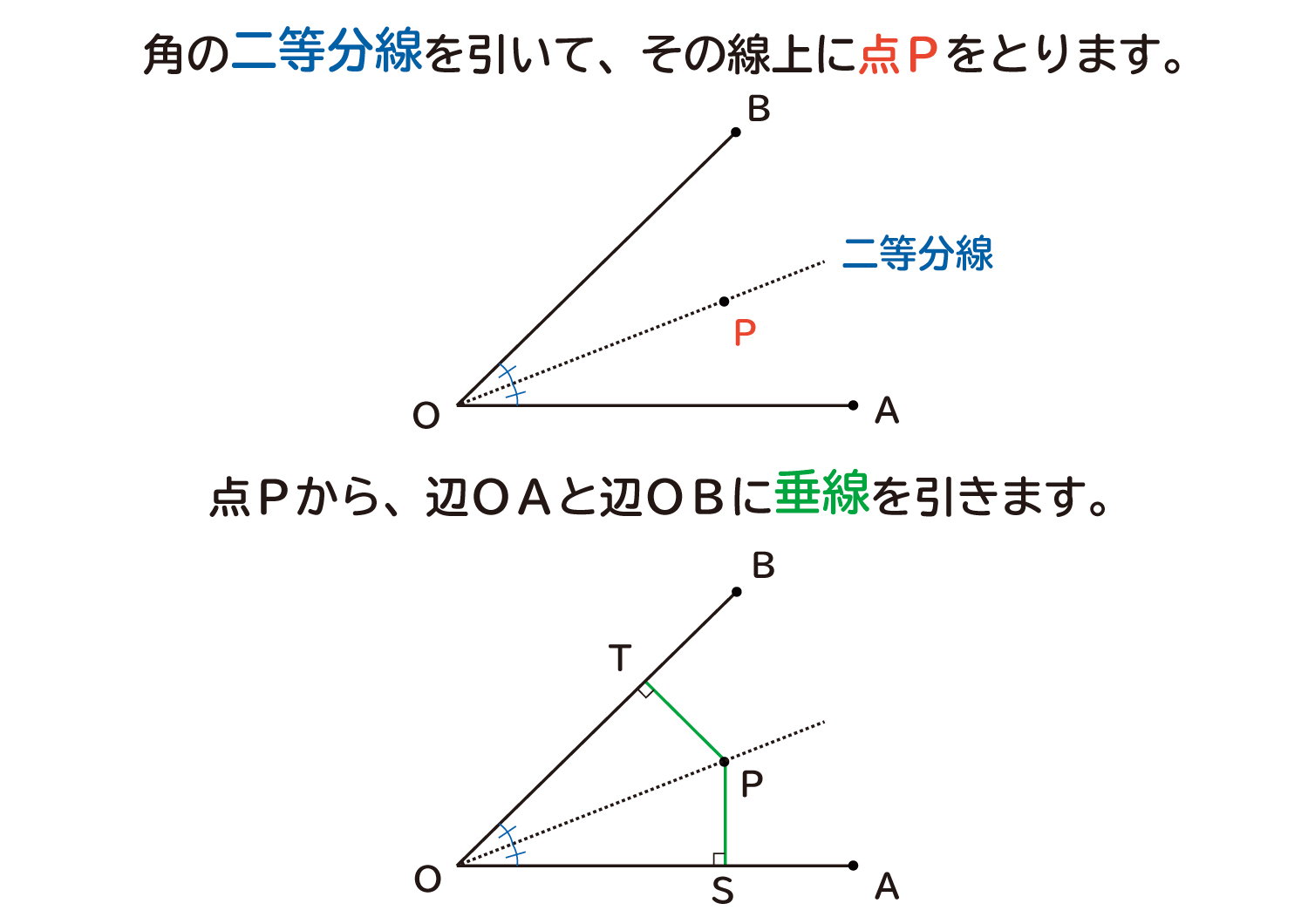
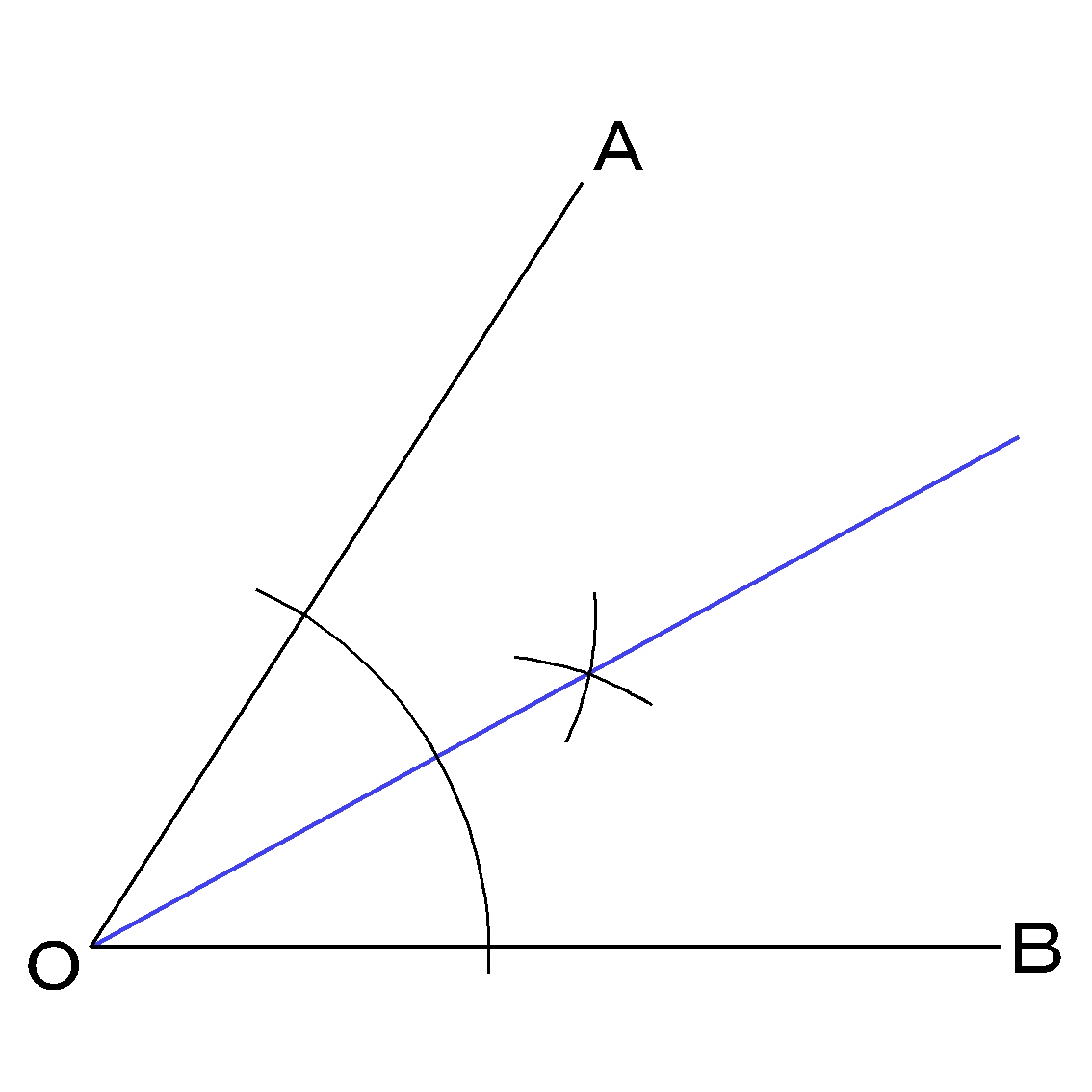
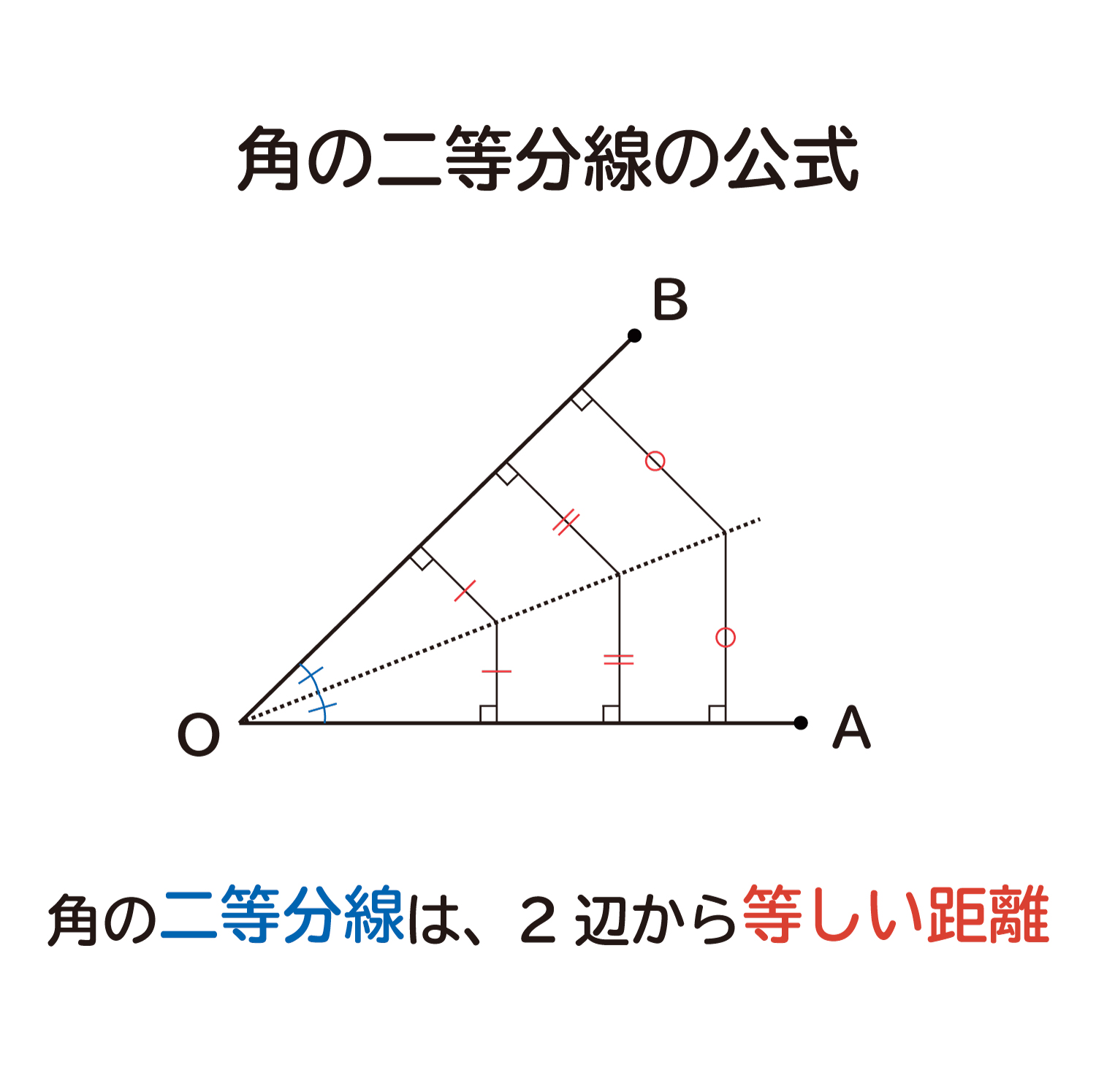
第135問 角の2等分線 図形ドリル 6年生 二等分線 回転移動 正方形 ★★★★★★(大人レベル) 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは,色々なタイプの図形問題を取り上げています。角の二等分線はただ一つしか存在せず、また、角の二等分線上の点から角を構成する直線への距離は同じになる。 二等分したい角を中心に二辺と交わる円弧を描いた後は、二辺との二つの交点から線分の垂直二等分線と同じようにして求めることができる。(図2.) 関連項目 定規とコンパス角の二等分線は、 2 2 つの直線から等距離にある点の集合です。 単純に、「 2 2 辺からの距離が等しい直線は角の二等分線」ともいいます。 垂直二等分線の作図と角の二等分線の作図。 必ず暗記しましょう。 これがすべての作図に通ずる超重要事項です
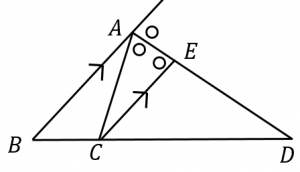
証明 Cを通りAQに平行な線とABの交点をEとし、BAの先をOとする。 AQとECは平行であるため錯角と同位角より ∠AEC=∠ACE=∠CAQ=∠OAQ よって AECは二等分線である。 なので AE=AC ① また EBC∽ ABQなので BQ:QC=AB:AE ②定規とコンパスを使って角を二等分する方法と更にもう一 つ\ある操作" を加えて三等分する方法をお話します。特に、 角の三等分は古代からの数学上の未解決問題の一つでした。 本講座では、実際に、定規とコンパスを使って作図してみま す。定規とコンパスをご準備ください。 1.二等分 2 ここでは、三角形の角の二等分線の長さを一派的な形で求めてみます。 標準三角比と角の二等分線で見た内容の一般化です。 目次 三角形の角の二等分線の長さ;



三角形の角の二等分線定理 外角
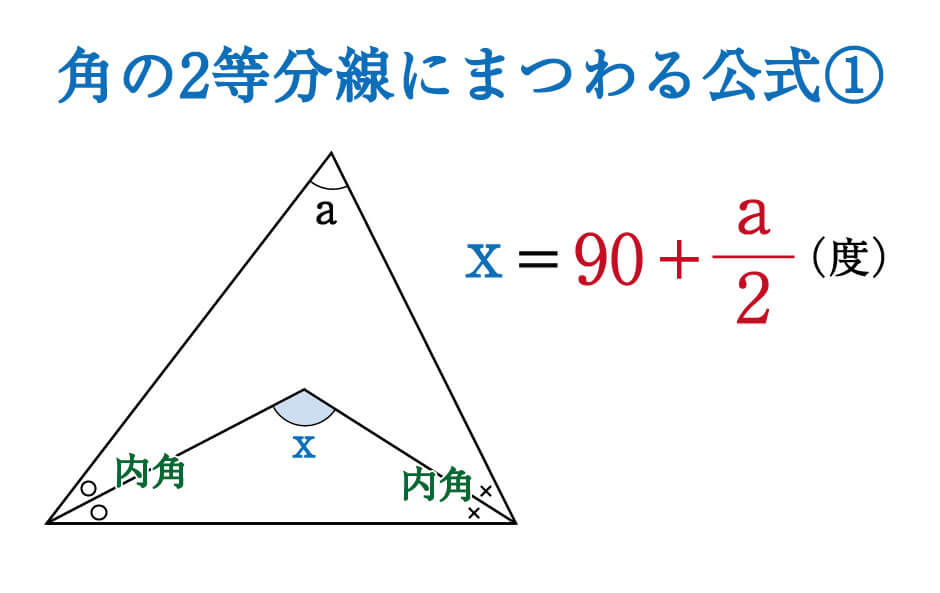



数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための 勉強サポートサイト Shuei勉強labo
角の二等分線という名の通り、角を二等分することを頭に置いておけば、とても簡単な作図ですね! 角の二等分線の証明 ここでは、角の二等分線の定理の証明方法を説明します。 証明①内角の二等分線の定理 内角の二等分線の定理は、「二等辺三角形の性質」と「平行線と比の性質三角形の角の二等分線は1点で交わるという証明は現在、中学2年生の 教科書(東書その他)にあります。 それぞれの角の二等分線は1点でまじわり、 点dを中心に円を書くと j dを中心に三角形の3つの辺に接する 円を書くことができます。この円を 内接円といい、中心を内心といいます。 下の(三角形の角の二等分線に関する公式2) (証明) CからADに平行な直線を引き、Abとの交点をEとする。 よって、 ACEは二等辺三角形、AE=AC。 ADとECが平行より、AB:AE=BD:DC、 AE=ACだから、AB:AC=BD:DC。
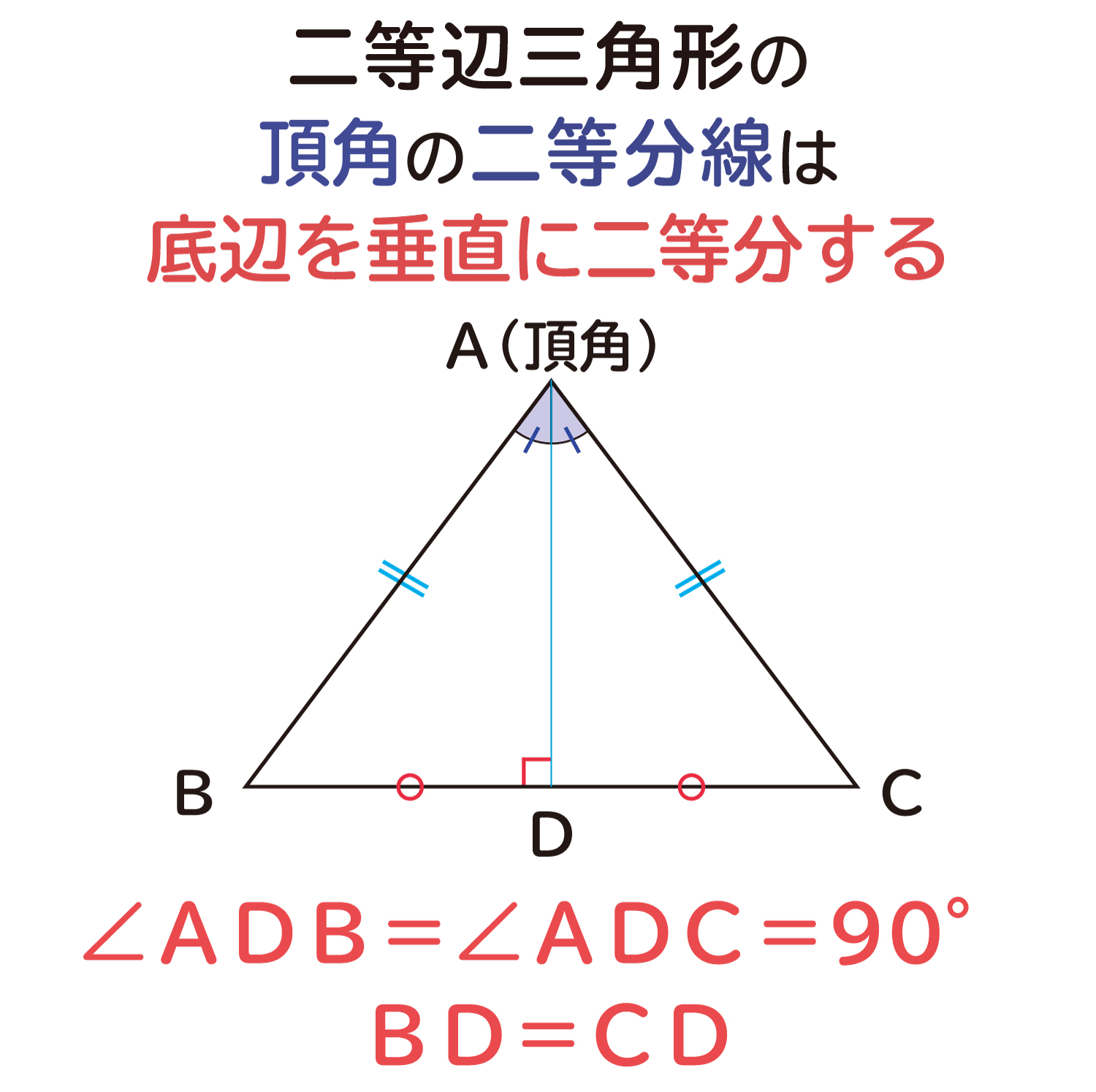



二等辺三角形の頂角の二等分線は 底辺を垂直に二等分する ことの説明 おかわりドリル




第1学年 平面図形 角の二等分線の作図の謎に迫る 生徒が持つ傾向を活かした授業展開 授業実践記録 アーカイブ一覧 授業支援 サポート資料 数学 中学校 知が啓く 教科書の啓林館
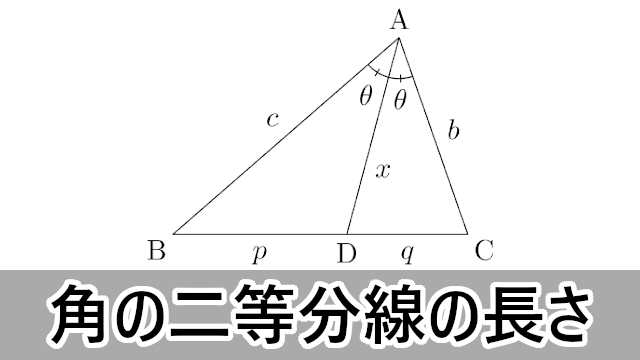
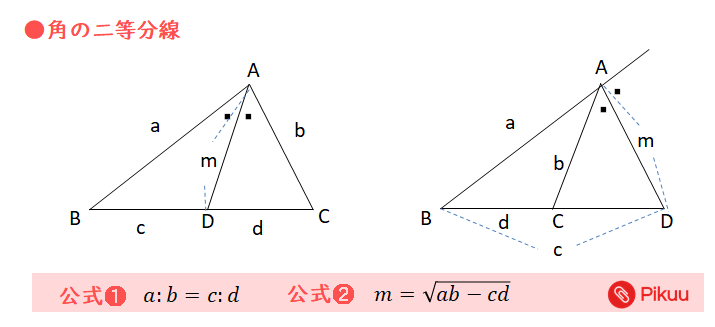
角の二等分線の作図 ・角が二等分される $\textcolor{blue}{\rm POINT}$ :二等分線は角をつくる $\textcolor{blue}{2}$ 辺から等しい距離にある 2:02 例題点を通る垂線を作図しなさい。 $\textcolor{blue}{\rm Step1}$ :点にコンパスの針をおき、線分を通る円を描く $\textcolor{blue}{\rm Step2}$ :交点 $\textcolor{blue}{aおわりに 広告 ※ お知らせ:筑波大学年度医学群医学類推薦数学第2問 を解く動画を公開しました。 三角形 角の二等分線に関する重要な3つの公式 D D とおく。 AB=a, AC=b, BD=d,DC=e, AD=f AB = a,AC = b,BD = d,DC = e,AD = f とおくとき以下が成立する。 公式1は辺の比の公式で教科書にも載っています。 公式2は暗記する必要はありませんが,導出方法は覚えておくとよいです




角の二等分線の長さ の公式の証明 怜悧玲瓏 高校数学を天空から俯瞰する




中学数学 三角形と角 二等分線と角 Youtube
ABC において,∠B の二等分線と対辺 AC の交点を求めます。 ↑ 外角の二等分線 † ↑ 注意事項 † ↑ 関連事項 † 幾何(中学校数学) \SuityokuNitoubunsen 4 添付ファイル Nitoubunsen02png 929件 Nitoubunsen01png 911件 Lastmodified (金) (3144d) Link 五十音順一覧(45d) 幾何(中学校数学)(563d) Bousin(2604dこれが、「角の二等分線」のかき方だよ。 垂直二等分線をかくためには、点Aと点Bを決めてやる必要があるよね。 この2点A、Bの決め方だけおさえれば、あとは 今までやってきた内容とまったく同じ というわけだね。 例題で実際に角の二等分線を作図してみよう。 この授業の先生 今川 和哉 角の二等分線上は、2辺からの距離が等しくなる。 という特徴がありましたね! 〇辺から等しい距離に ときたら、角の二等分線を使うようにしてください。 詳しくはこちらの記事でも解説しています。 >中1 作図3辺から等しい距離にある点の作図方法とは? 角の作図 〇°の作図をせ




角の2等分線の定理 数学i フリー教材開発コミュニティ Ftext




中学数学 中学入試 平面図形と角 二等分線と角 Youtube
とし,BCとの交点をPとすると PB:PC=AB:AC である. 証明 頂点B,頂点Cから二等分線 ℓ 角の二等分線というのは、角を二等分している他にも次のような特徴があります。 角の二等分線上の点は、角の2辺までの距離が等しい。 角の二等分線上の点は、どこをとっても2辺からの距離が等しくなっています。 なので、 2辺から等しい距離にある点を作図せよ。 という場面でも角の二角の二等分線 の部分一致の例文一覧と使い方 該当件数 31 件 例文 ハンドルの中心 線 は 二 つの固定接触面1の交わる 角の二等分線 である。 例文帳に追加 The center line of the handle is a bisector of the crossing angle between two fixing contact surfaces 1 特許庁



角の2等分線の方程式 数学の偏差値を上げて合格を目指す
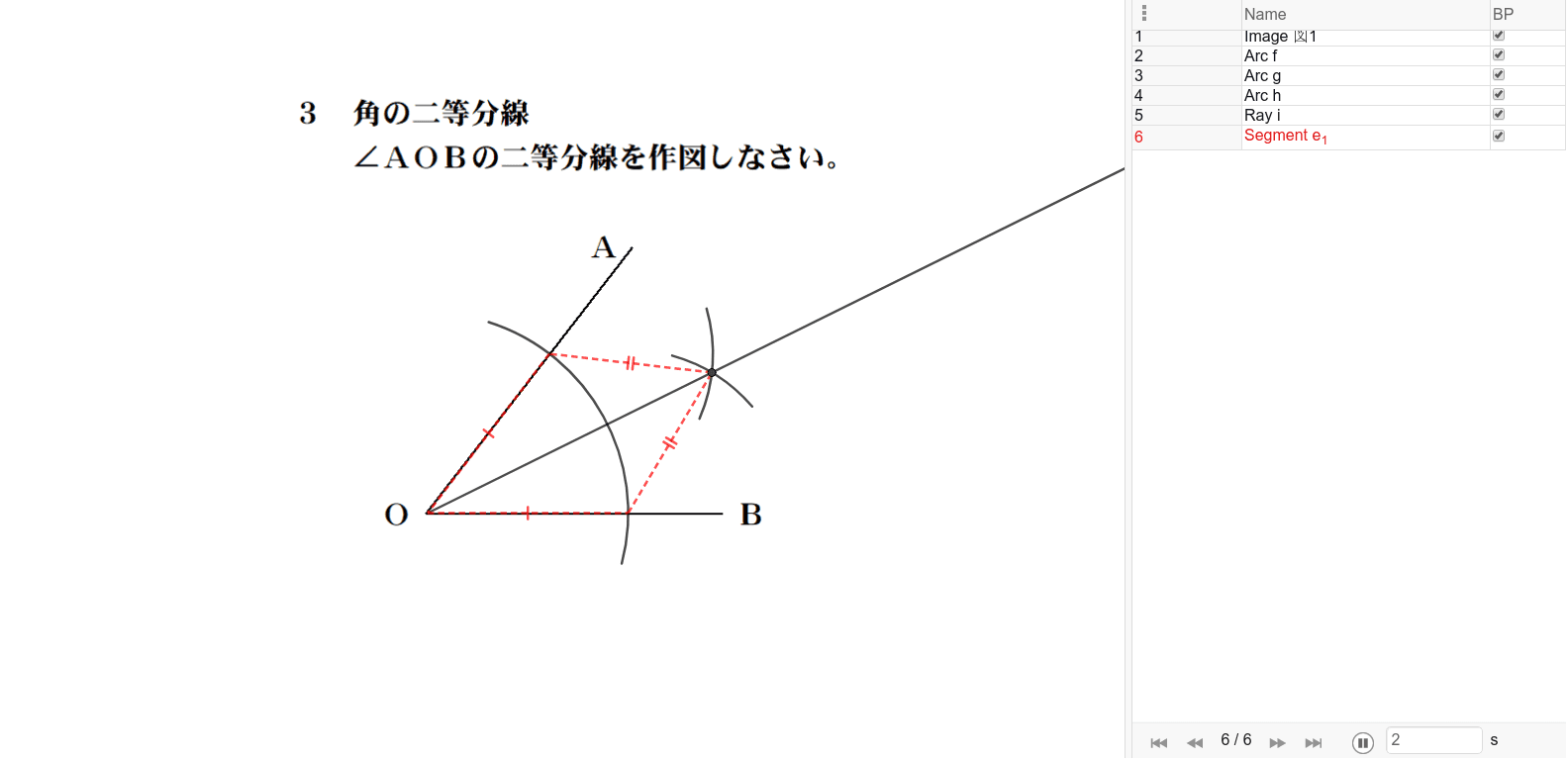



角の二等分線の作図 Geogebra
前回 https//wwwyoutubecom/watch?v=q78K0dnUwug&index=22&list=PLKRhhk0lEyzOfDE8u9U0GWX3aa43XeMOr 次回 https//wwwyoutubecom/watch?v=IWKH_iqBkco&list角の二等分線 の作図手順 コンパスの針を角の頂点Bに合わせ、それぞれの線分と交わるような弧を描く 交わった点を中心とした同じ半径の弧を描く 弧どうしが交わった点と角の頂点Bを結んだ線が角Bの二等分線となる 二等分線の性質の逆 角の二等分線の長さ 三角形の内角・外角の二等分線の性質は,中学数学で習う基本的で重要な性質です.それらの主張とその証明を紹介します.さらに,後半では発展的内容として,角の二等分線の長さについても紹介します. ⇨
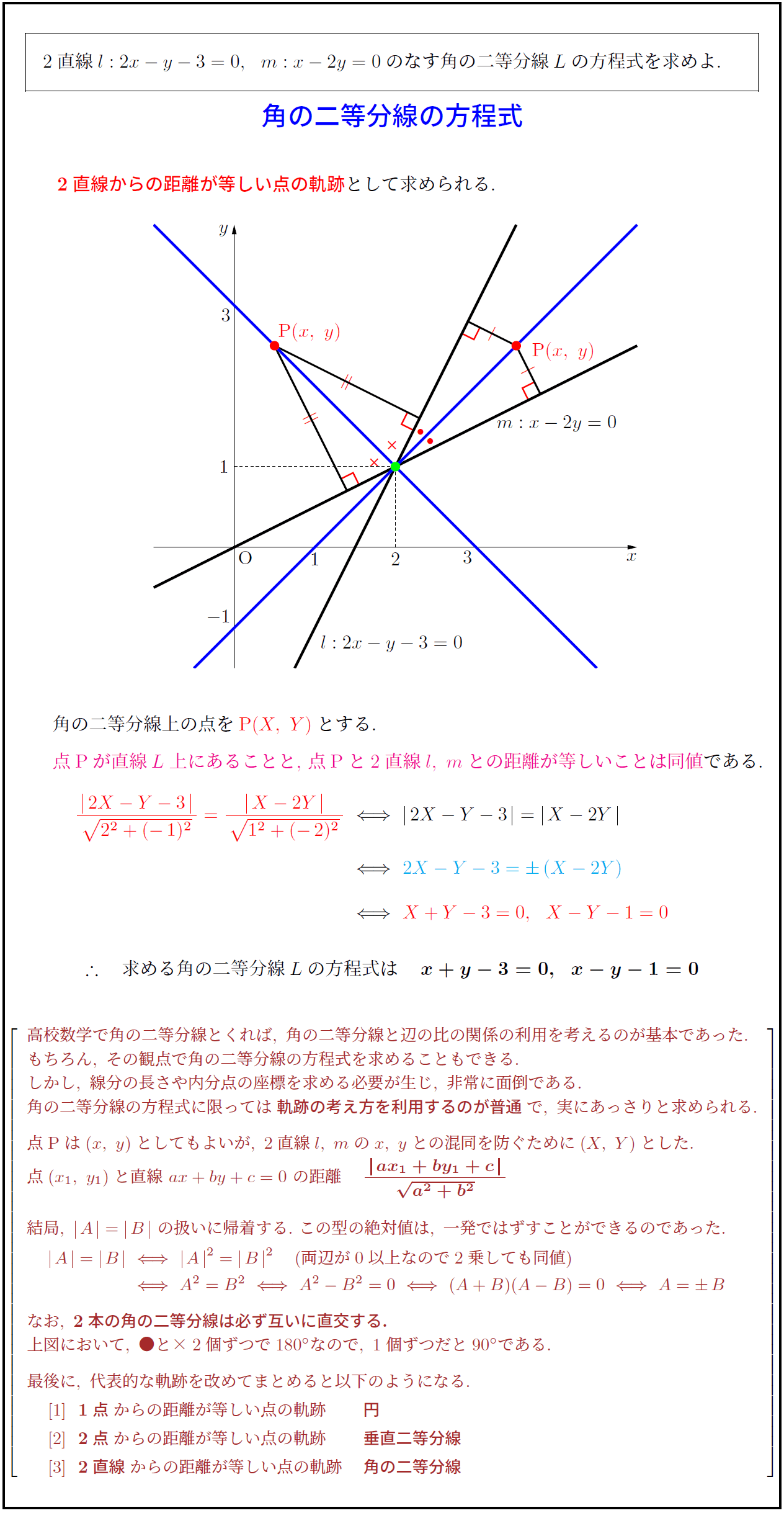



高校数学 角の二等分線の方程式 軌跡の利用 受験の月



三角形の角の二等分線定理
ハンドルの中心線は 二 つの固定接触面1の交わる 角の二等分 線である。 例文帳に追加 The center line of the handle is a bisector of the crossing angle between two fixing contact surfaces 1 特許庁 第1のスキームにおいて、経由孔は、コネクタ基板の調整不良 角 度を 二等分角度を単位円上の点として扱う幾何代数の技法によって、角の二等分線の性質を確認します。 クリフォード代数は使用しないで、複素平面上でオイラーの公式に基づく計算を行います。 ※ 図は Markdown に SVG を直接記述しています 角の二等分線定理の練習問題 (4)図のようには、ab=8、ac=6、∠bac=60°の abcがある。∠bacの二等分線と辺bcの交点をd、点cを通りadに平行な直線と辺baの延長の交点をeとする。bd:dcをできるだけ簡単な整数比で表しなさい。 角の二等分線定理の解答 (1)DE=2 CP=40/7 (2)3:2 (3)2:5 (4)4



角の2等分線



角の二等分線定理 内角 外角それぞれ 具体例で学ぶ数学
角の二等分線の性質は高校数学Aの教科書で登場しますが,数学Aの中で平面幾何を選択することはほとんどないため,この定理に接する機会はめったにありません. ≪注意すべきこと≫ 右図2では d は bc の中点ではありません.右図2のように頂点 a が右寄りになっているとき∠ bad= ∠ dac とした高校数学の要点, 無料の練習問題, 例題と解説 角の二等分線角の二等分線と比とその証明 内角の二等分線と外角の二等分線と公式が $2$ つあるので順に紹介します. ポイント 内角の二等分線と比 $\triangle \rm{ABC}$ で ${\rm AB}=a$,${\rm AC}=b$ とする.$\angle \rm A$ の内角の二等分線と直線 $\rm BC$ の交点 $\rm P$ において $\boldsymbol{{\rm BPPC}=ab}$ 上の公式は暗記




高校数学a 角の二等分線と比の利用 練習編 映像授業のtry It トライイット




高校数学 数 98 三角形の内角の二等分線 Youtube



角の二等分線定理 内角 外角それぞれ 具体例で学ぶ数学



数学ia 三角形の内角の二等分線の長さ 大学入試数学の考え方と解法




角の二等分線と比の定理とは 作図方法 書き方 や性質の証明を解説 外角の問題アリ 遊ぶ数学



3分で分かる 角の二等分線とは 定理 証明やその性質をわかりやすく 合格サプリ



見えない角の二等分線 の問題です 画像のように2本の直線a B Yahoo 知恵袋




サクッと解説 角の二等分線と比の特徴となぜ について 数スタ




重心を通る直線 角の二等分線ですか Clearnote



1




角の2等分線によって分ける比 身勝手な主張
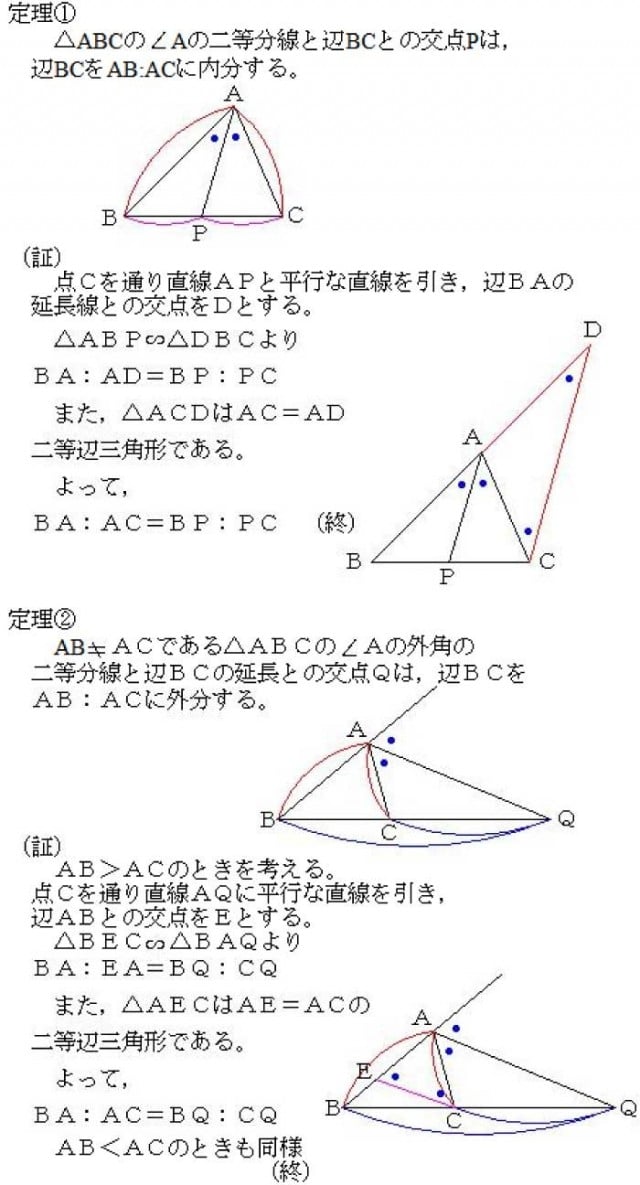



三角形の角の二等分線と比
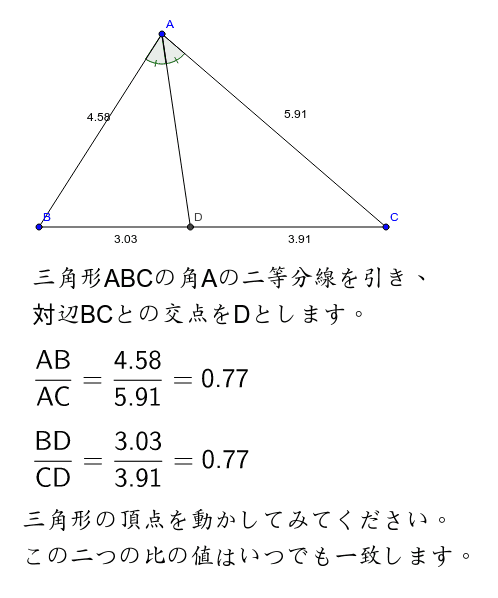



三角形の内角の2等分線と対辺 Geogebra
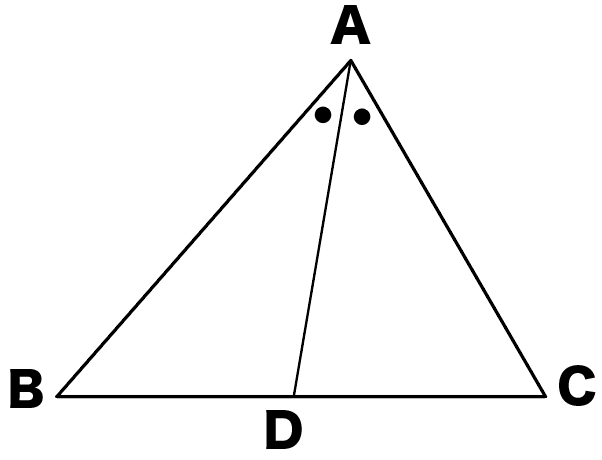



三角形の角の二等分線の性質 定理の証明がわかる5ステップ Qikeru 学びを楽しくわかりやすく



角の二等分線 まなびの学園



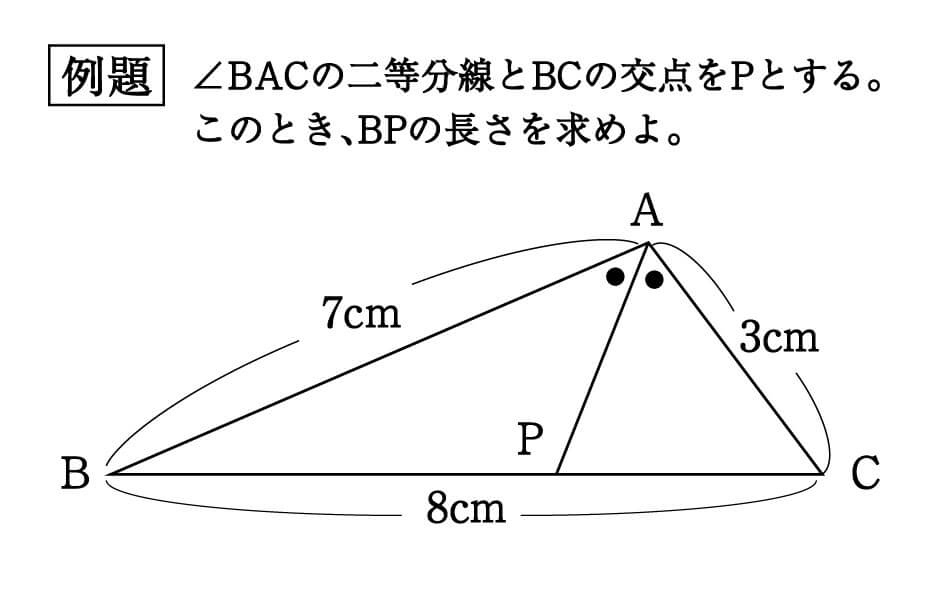
中3数学 角の二等分線と線分比 2 Youtube
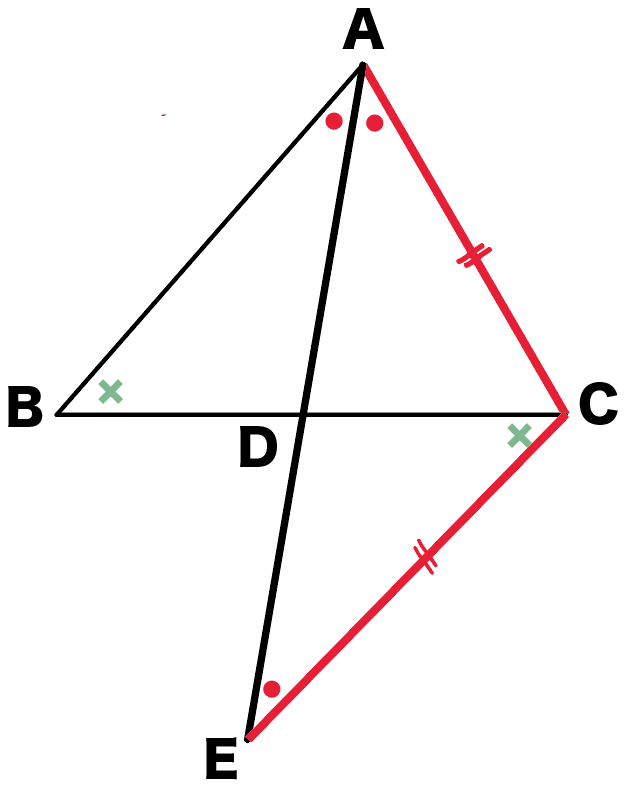



三角形の角の二等分線の性質 定理の証明がわかる5ステップ Qikeru 学びを楽しくわかりやすく



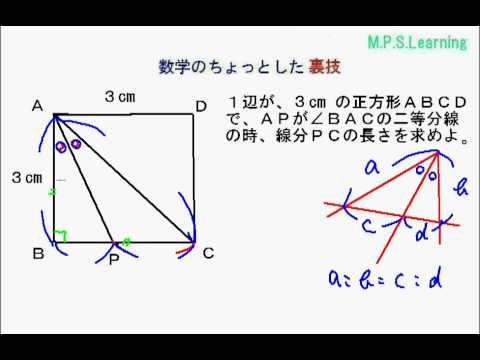
数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための 勉強サポートサイト Shuei勉強labo
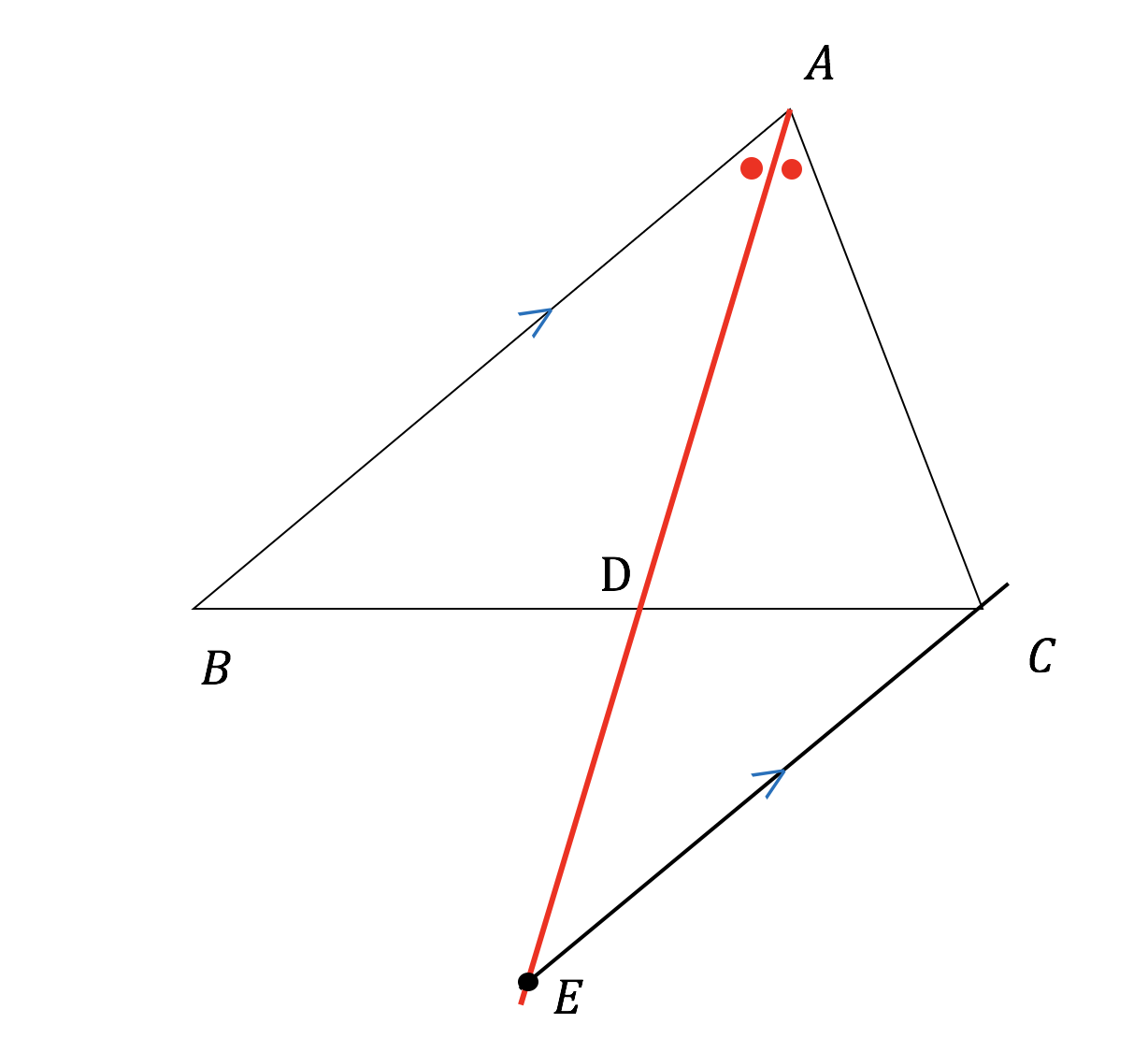



3分で分かる 角の二等分線とは 定理 証明やその性質をわかりやすく 合格サプリ




頂角の二等分線は底辺を二等分する Youtube



角の二等分線定理 内角 外角それぞれ 具体例で学ぶ数学



角の二等分線 作図




高校数学b 角の二等分線のベクトル2パターン 受験の月



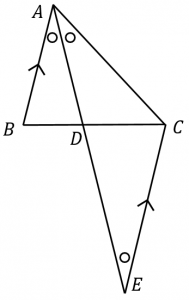
中学数学 角の二等分線定理の高校入試対策問題 Pikuu



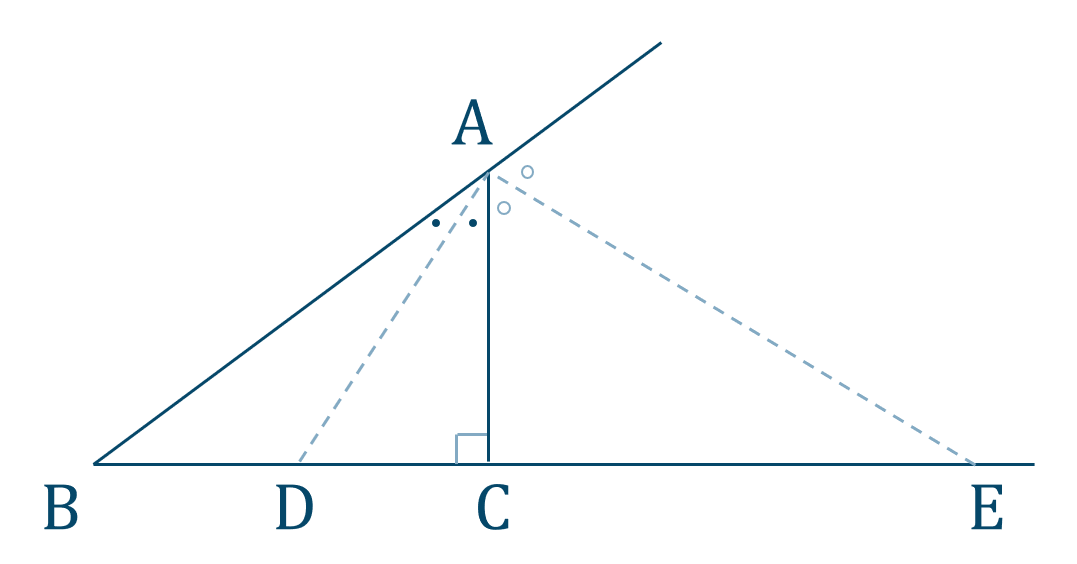
なぜ 角の二等分線は その角を作る2辺から等しい距離 なのか を説明します おかわりドリル




角の二等分線が図で誰でも一発でわかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ



角の二等分線 Wordで数学問題プリントを作ろう
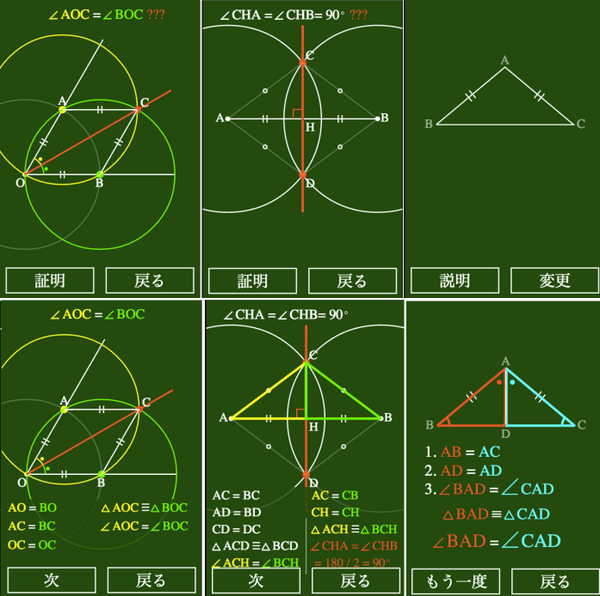



すうがくぼっと 体験宣伝ボット V Twitter 603mayu 突然だけどよかったら 基礎的な証明 角の二等分線 垂直二等分線 二等辺三角形 の底角 ウェブサイトやアプリで図形力を Http T Co Izmtqmy7o1 Http T Co Bi5quiyfbx
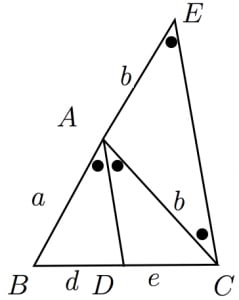



角の二等分線に関する重要な3つの公式 高校数学の美しい物語
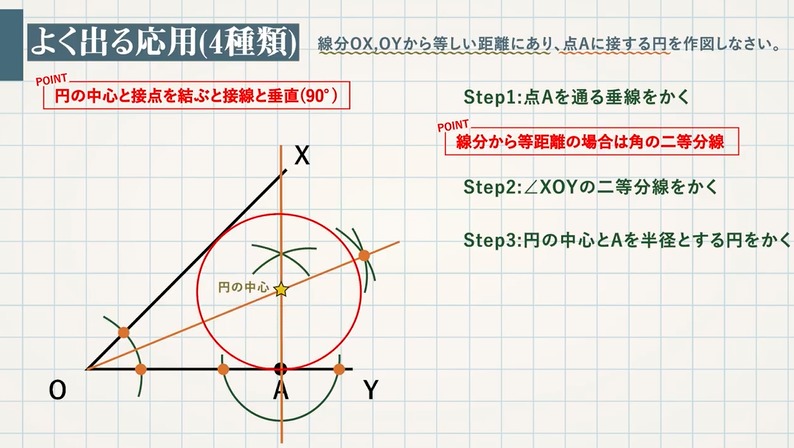



1年生で習う作図まとめ 教遊者




角の二等分線に関する問題 一目瞭然早見チャート 高校生 数学のノート Clearnote
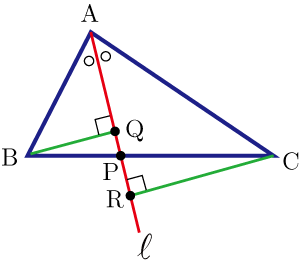



三角形の頂点の二等分線の性質
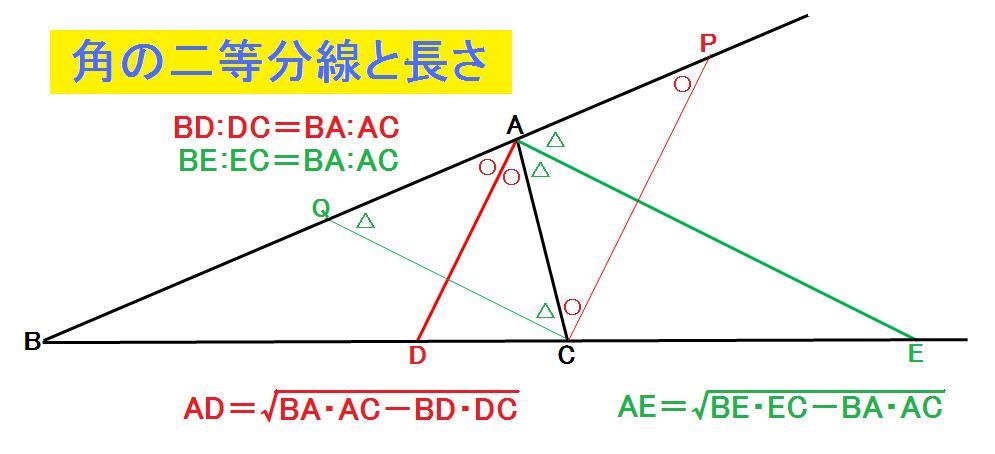



角の二等分線の長さの公式 ヤドカリの 気ままな数学




ベクトル方程式 角の二等分線 数学の偏差値を上げて合格を目指す




角の2等分線の定理 数学i フリー教材開発コミュニティ Ftext
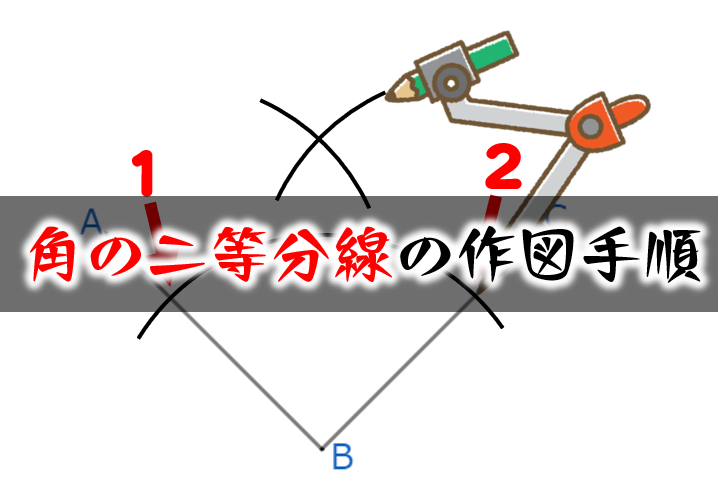



角の二等分線 の作図方法 コンパス 定規 数学fun




角の2等分と線分の比 中学数学の無料オンライン学習サイトchu Su




基本 角の二等分線の作図 なかけんの数学ノート



中3数学 角の二等分線定理のポイントと練習問題
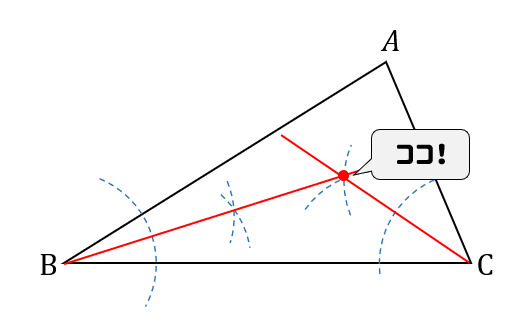



作図 角の二等分線のやり方は どんな問題で使えるのか解説 数スタ



3




角の二等分線定理の証明 学びをつづる
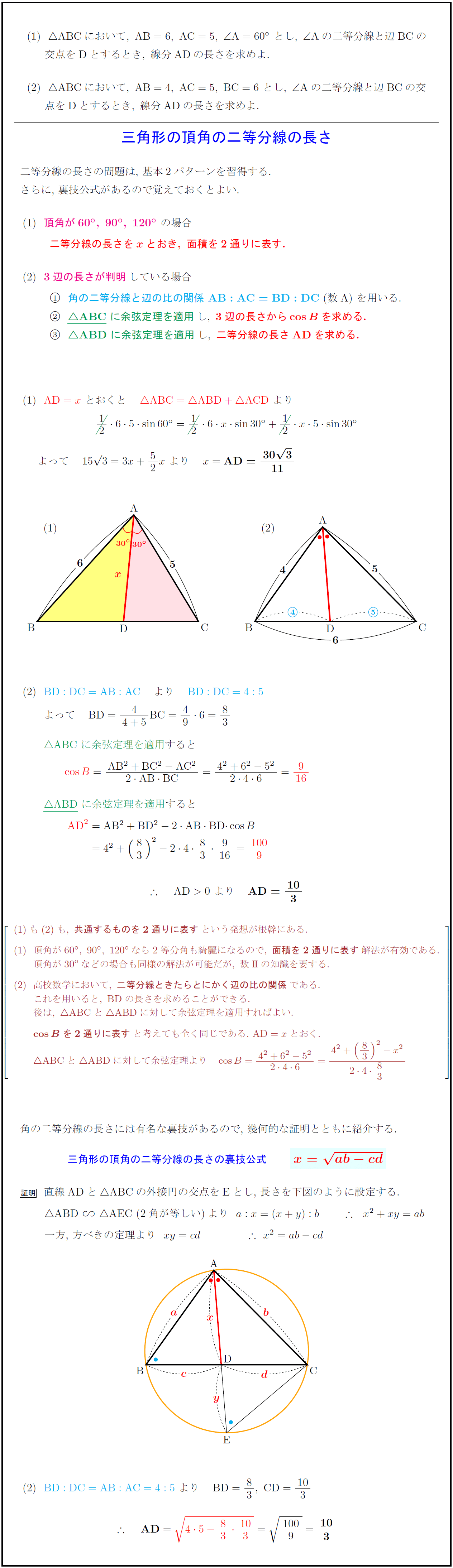



高校数学 三角形の頂角の二等分線の長さ 基本2パターン 裏技公式 X Ab Cd とその証明 受験の月




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
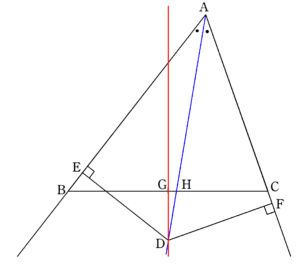



二等分線と垂線の定理 Fukusukeの数学めも



内接円 内心




基本の作図 5ステップでわかる 角の二等分線の書き方 Qikeru 学びを楽しくわかりやすく




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



Math 平行と合同 角の二等分線と角度 働きアリ The 2nd
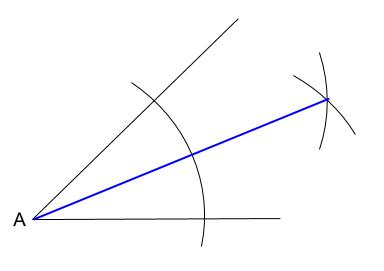



中学数学 作図 垂直二等分線 角の二等分線 中学数学の無料オンライン学習サイトchu Su



平行四辺形の角の二等分線
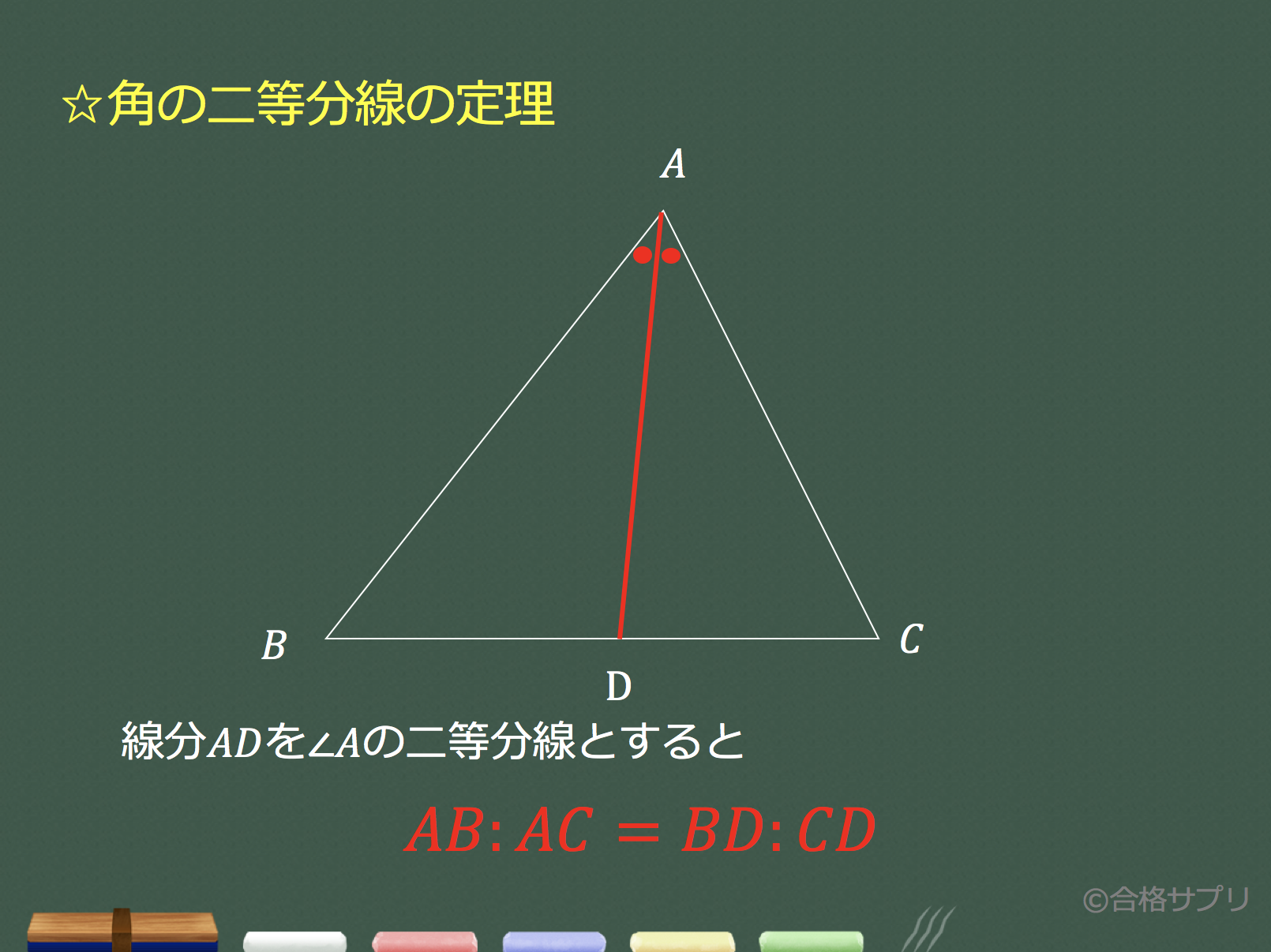



3分で分かる 角の二等分線とは 定理 証明やその性質をわかりやすく 合格サプリ
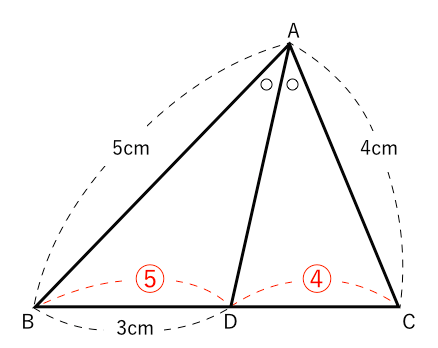



相似な図形 角の二等分があったらこれ 苦手な数学を簡単に
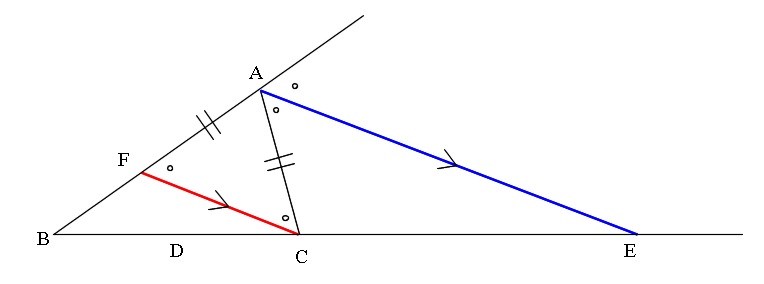



内角の二等分線と外角の二等分線の定理の覚え方と使い方



簡単にわかる 角の二等分線を作図する方法 苦手な数学を簡単に




角の二等分線の性質 線分比の公式 に関する定理の証明 理系ラボ



角の2等分線



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典



角の二等分線の長さを求める公式 ほのぼの数学頑張ろう



Math 平行と合同 角の二等分線と角度 働きアリ




数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための 勉強サポートサイト Shuei勉強labo
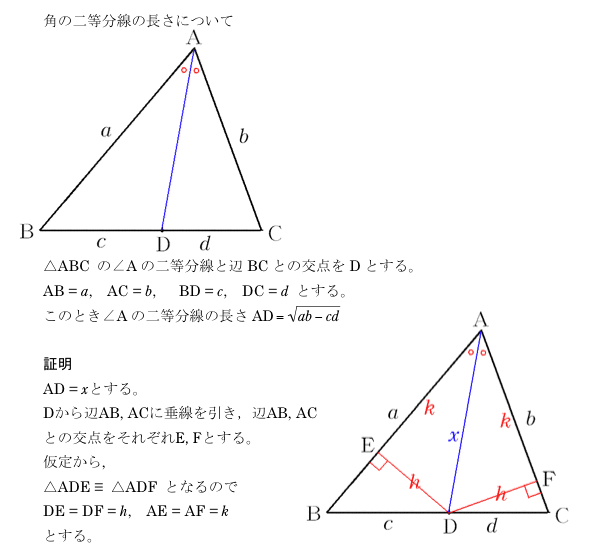



角の二等分線の長さ Takapの数学日記




角の二等分線が図で誰でも一発でわかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ
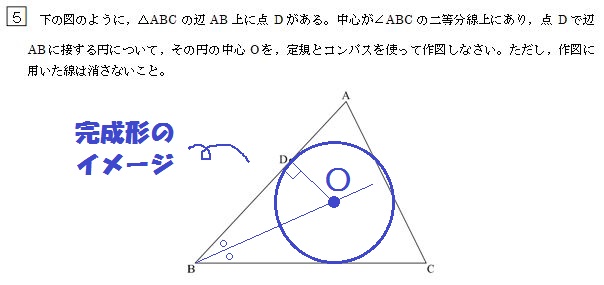



中学数学 平面図形 のコツ 角の二等分線 垂線を使った作図




基本 三角比と角の二等分線 なかけんの数学ノート




三角形の二等分2パターン 角の二等分 中線定理 数学の偏差値を上げて合格を目指す



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学



2




勉強しよう数学 角の二等分線の長さ 相似図形による定理の証明



学んでいて感じる疑問 Ssブログ




複素数平面での幾何学を勉強してる際 有名な 角の二等分線の定 人力検索はてな




基本 軌跡 垂直二等分線や角の二等分線 なかけんの数学ノート



数学a 角の二等分線と比の使い方とコツ 教科書より詳しい高校数学




見えない角の二等分線のやり方 見えない角の二等分線とは 普通の角の 中学校 教えて Goo




角の二等分線の作図 Youtube



角の二等分線に関する問題 中学受験 田中貴 Com



1



傍接円 傍心について



なぜ 角の二等分線は その角を作る2辺から等しい距離 なのか を説明します おかわりドリル



長さの比 角の二等分線の定理 浅野中学 13年 どう解く 中学受験算数




三角形の角の二等分線の長さ 中学数学教材研究ノート
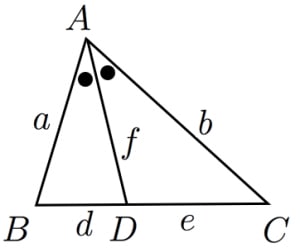



角の二等分線に関する重要な3つの公式 高校数学の美しい物語




高校数学a 外角の二等分線と比 練習編 映像授業のtry It トライイット




作図の3種類 垂直二等分線 角の二等分線 垂線 は 実は同じ図形だ 東大に文理両方で合格した男が綴る 受験の戦略



角の二等分線の書き方 学活ブログ



角の二等分線をひく 中学から数学だいすき
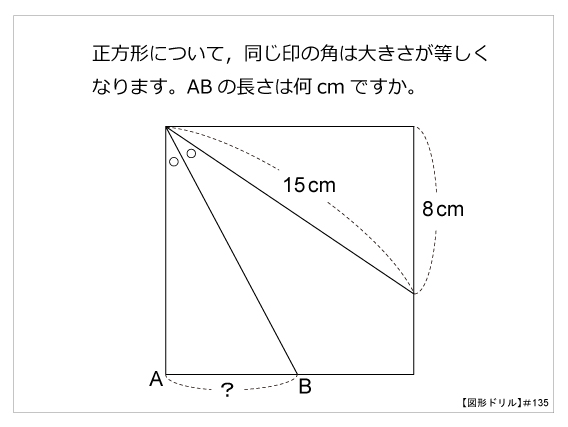



第135問 角の2等分線 図形ドリル 第135問 角の2等分線 算数星人のweb問題集 中学受験算数の問題に挑戦
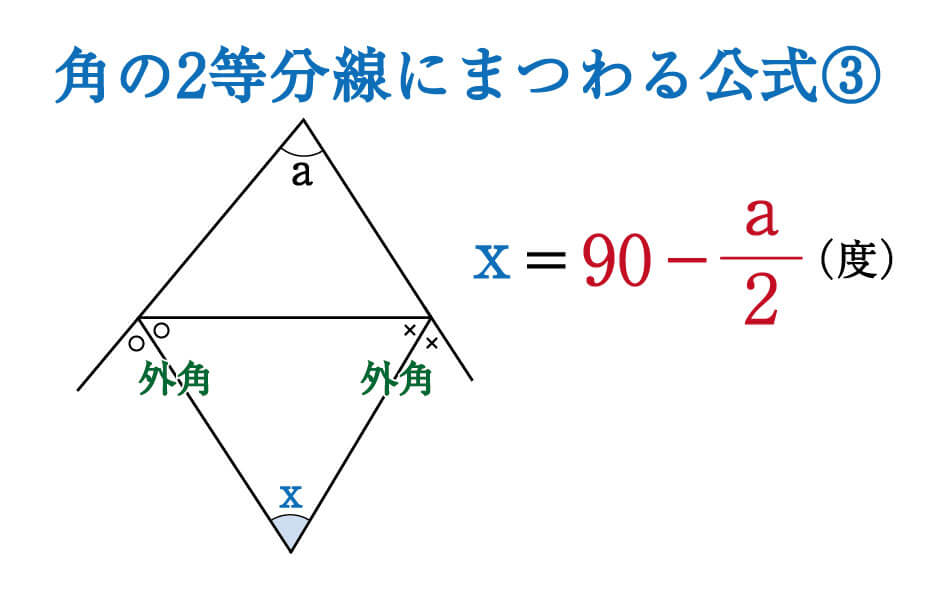



数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための 勉強サポートサイト Shuei勉強labo




角の二等分線に関する定理 高校数学の知識庫



Studydoctor角の二等分線の作図と利用 中学1年数学 Studydoctor
コメント
コメントを投稿